
Contemporary research has now proven that the ‘ignorant savage’ story distorts a more complex reality in which the natives viewed their strange guests as the gullible party parting with decorative items. As a matter of fact, the historical record shows axes, iron kettles, and woollen clothing exchanged for what were, to the local inhabitants, almost worthless beaver skins, often worn and ready to be thrown out, or signatures on title deeds to property, which meant nothing to the locals who entertained no concept of land ownership. Both sides in this historic barter were astonished at the preferences of the other.
Equally, criticisms seem to be bidirectional when it comes to statisticians and the other ‘tribes’ with whom they collaborate, so to speak. From the wealth of analytical tools that end users of statistics need only ask for, there seems to be, from the statisticians’ viewpoint, an ill-informed clamour for items of dubious merit in preference to the high value items that ought to be craved. The process of exchange, as in our historical example, seems continually challenged by communication issues and lost-in-translation episodes, making early stages of collaboration hard going, as all engaged in these transdisciplinary voyages of discovery will be well aware.
Two particular communication break-downs have intrigued me throughout my years as a statistician, from student days into my professional life. On the one hand, I have become accustomed to hearing time and time again the misconception that statistics is “all about probabilities”. Any reputation statistics has, then, becomes tarnished in the face of an unexpected turn of events such as rain on your wedding party after a forecast of a sunny day, which is routinely taken to invalidate the judgement that the outcome was improbable. While true that there is an important side to statistics that focuses on predictions, its main role of interpreting what data is saying and telling a story that is both understandable and relevant to its audience is often overshadowed by this sort of wrong-headed thinking.
On the other hand, when talking to fellow, young practitioners, a common complaint seems to arise regarding the search for significance on the client´s side.
To illustrate this idea, I recently introduced myself as a statistician to a new acquaintance who’s first thought was to enquire what my favourite statistical test was. Although my immediate reaction was to smile, it got me thinking. Not only did it make me more conscious of the association of tests with statisticians being common-place, but it also made me wonder whether we all have some sort of favouritism that can lead us to apply one test rather than another.
Are, for instance, particular tests in the ascendency in specific disciplines? Apart from the obviously varying requirements of different sorts of data and experiments, scholarly publications on the matter seem to have reached a consensus regarding tendencies towards different underlying rationales for statistical testing in the various areas of research.
The German psychologist, Gerd Gigerenzer1 writes about the variation in selection and application of statistical tests across disciplines. In the social and behavioural sciences he sees tests being deployed in order to ‘prove’ hypotheses assuming that the data is accurate. Conversely, the ultimate aim of statistical tests in the natural sciences he identifies with the detection of unusual patterns given that the theories are true. In particular he mentions t-test and F-test as the most commonly used amongst psychologists. An economist and management scientist, David A. Gulley2, makes a related observation about “best-known tests” identifying the precursor F-test as an exemplar of a favoured method in natural sciences. Keuzenkamp and Magnus3 refer to nuclear physics as one of the fields in which the quality of fit tests (e.g. Chi-square) between theory and the results from practical experiments are not in use, physicists instead draw their final conclusions from qualitative arguments.
In areas such as finance and management science, the authors highlight the prevalence of tests that inform decision makers.
By way of illustration of these variations, consider the following sample research questions that could be associated with three of the aforementioned fields.
Sociological research addresses the nature of society. For example, they could be comparing the social interactions of big supermarkets’ shoppers with local shops’ clientele to try to find statistically significant differences with respect to their relationships with their neighbours.
In the case of natural scientists, a focus on physical characteristics might result in them asking whether tomatoes sold in supermarkets contain the same amount of water as those coming from local farmers.
Finally, economists might look at the problem in terms of profitability, for example, is it more advantageous for supermarkets to sell organic tomatoes rather than non-organic ones?
In each of these three cases, an unequivocal answer to the specific research question would not necessarily constitute an accurate test of any underlying hypothesis, as it might fail to reflect the wider context or might not be accounting for the real complexity of the phenomenon under investigation. Therefore, the initial sparkle of a straightforward answer can be blinding to researchers.
General requirements for the appropriateness of the procedures might be at risk. For instance, the sociologist might have only been able to speak to five of the consumers in each of the shops and therefore it would be difficult to extrapolate this to a more general population due to the small sample size. Alternatively, the majority of the shoppers going to a particular store might be local residents and might consequently share some unknown relationship interfering in the generalizability of the results. Hence, the ‘warmth’ that bigger samples provide might end up tempting the statisticians to discard more relevant or better designed experiments.
Social media can also show you how the public views the statistical profession. When looking for frequency patterns of the appearance of the word “statisticians” on Twitter (see below), apart from the comforting “Statistics don’t lie” (in bright pink), the expected “chances [of] lottery winning” (in green) and an association with the results from the Eurovision song contest (held on the previous day to this analysis), some interesting statements can be found
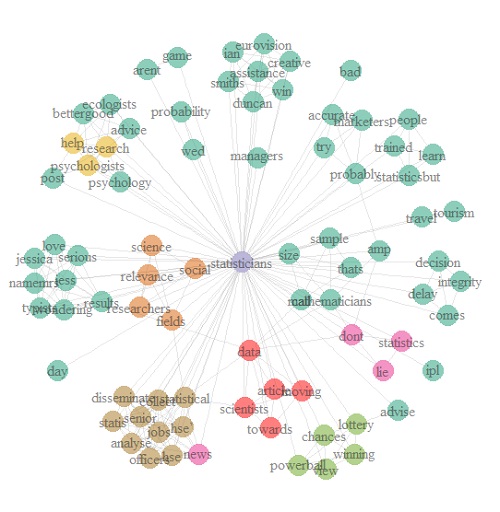
“Scientists moving towards data” (red) and “Better advice [to] ecologists” refer directly to the relationship between statisticians and other scientists. The first one would seem to support the approach of scientists toward statistics, and the second could be understood as a need for improvement from the statistical side.
In a similar fashion, two clear statements appear relating to the social and behavioural fields. “Social relevance [of] science” (orange) might represent the promotion of the benefits to society from statistical science, whereas “Help psychologists [with] research” (yellow) appears to be, again, a direct request for effective means of support.
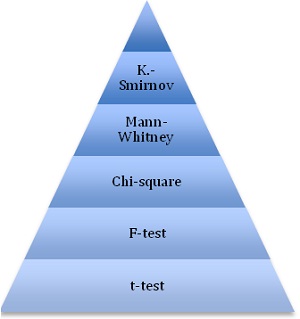
In terms of visibility of the different tests, the ranking seems ironically to be in inverse proportion to the obscurity of the name of the test with simpler, more memorable names preferred over longer, more difficult to digest names (see chart below). The highest search results are for t-test, F-test, and Chi-square consecutively, whereas only a few counts appear for Kolmogorov-Smirnov, just 2 for Kruskal-Wallis, and none for Wilcoxon.
Support for this criticism lies in the very foundations of statistical testing. In Fisher´s celebrated “lady tasting tea experiment” a subject’s proficiency in distinguishing whether the milk has been added before or after the tea (a skill the lady claims to have mastered) is put to the test within eight sample cups; four in which milk was added before tea and four with the reverse combination. The experiment demonstrates that any experimental success the lady might produce cannot rule out other reasons for her correctly detecting the difference, including chance or cheating. In short, reaching significant results in scientific experiments does not necessarily validate the initial hypotheses.
Major emphasis should be placed on background knowledge and toolkits of both statisticians and researchers in order to reach a consensus around the real problem under study, generally of a larger scope than a single yes or no answer.
It remains to be answered whether this tendency towards ubiquitous testing in general and the widespread use of certain tests in particular, is largely being seen as a guarantee of accuracy for publication purposes rather than fulfilling a real need in many cases.
I also wonder whether the alternatives are being properly explained and understood. If when consulted on the appropriateness of certain tests, a new ‘alien’ technique is suggested whose application and inference-making process are more subjective and require further statistical knowledge, it is quite likely that the user will despair and run back to the comfort zone of statistical tests and guided interpretations. In order to avoid this retreat to the safety blanket, trust generation appears the likeliest solution. In the same way that we ask the patient to trust the doctor, and keep taking the new tablets even with unpleasant side-effects, so we want to persuade scientists to adopt new, tricky statistical methods that might initially give them a headache, but would provide them with a long-term solution.
All of the above highlights the need for new thinking. Greater importance should be given in early stages of the career development of statisticians to imparting communication skills and developing new forms of knowledge exchange to ensure that the true benefits of statistics come across fully in multidisciplinary teams.
Now that the cultural myth of ‘beads for Manhattan’ has been blown apart by modern scholars of history, showing that both sides had valid reasons for choosing such dissimilar objects as currency, we might similarly reconsider our reading of knowledge exchange in our own field.
A new mentality should spread in statistics and the other sciences. On the one hand, statisticians should acknowledge that real-life experiments require big efforts and might not necessarily ensure that big sample sizes or independence of observations are achieved. On the other hand, although the application of tests to ascertain hypotheses in certain situations is undoubtedly one side to our profession, and probably the shiniest trinket of all, it is our responsibility to explain to other researchers the advantages of alternative techniques and deeper approaches. It is in our hands to show all the treasures that statistics hides.



