
Politics is, by definition, adversarial. Its systems are designed to bring together people with competing views, so that they might argue over and decide on the “affairs of the cities” – which is the literal translation of the Greek word πολιτικά (Politiká). But, in recent times, politics has felt like it has become more adversarial, more polarised.
People on different sides of an argument seem entrenched in their views, and appear not to take the time to listen and carefully consider what their opponents are actually saying, with discussions – in the House of Commons, on TV and radio, and particularly on social media – often descending into mud-slinging.
In the UK, emotions are running high as Britain’s exit (or Brexit) from the European Union (EU) seemingly approaches. With the country broadly divided between “Leavers” and “Remainers”, there are many examples of this sort of polarized political discussion. Consider this example from a BBC broadcast in March, in which journalist and Remainer, Will Self, and the Conservative politician and Leaver, Mark Francois (both pictured above), trade verbal blows without stopping to think carefully or respond logically to the points being made:
Will Self: “Every racist and anti-Semite in the country pretty much probably voted for Brexit.”
Mark Francois: “You’ve basically tried to slur anybody who voted Leave as a bigot.”
Now, Self has made a sweeping claim without offering evidence by way of support, and we’ll come to that later. But, first, let’s consider this: is Francois correct in his assertion? Has Self tried to slur all Leave voters as bigots? Or has Francois committed a fundamental error of statistical reasoning?
The prosecutor’s fallacy, and more
From the statistical point of view, there are several interesting and subtle aspects hidden in this seemingly simple but heated exchange. What Self is more or less explicitly referring to is the probability that somebody taken from the population of all racists and anti-Semites (I will label this as RaS), voted to leave the EU (L), which in formula is written as Pr(L ∣ RaS). Conversely, Francois interprets Self’s statement as a quantification of the probability that somebody chosen from the population of those who voted leave is racist or anti-Semite, which can be written as Pr(RaS ∣ L).
This contorting of Self’s argument by Francois is a classic example of the prosecutor’s fallacy. This terminology, derived from the legal jargon, indicates the case in which the probability of the evidence produced in court, say E, conditional on the hypothesis that the defendant is guilty, Pr(E ∣ G), is misinterpreted by the prosecutor as the probability that the defendant is guilty given the evidence, Pr(G ∣ E). This latter quantity represents the actual objective of the legal evaluation, but that is, in general, numerically different.
To formally see where the confusion lies, we can use the basic rules of probability calculus to factorise the joint probability of two events of interest – RaS and L, as specified above – in the two mathematically equivalent ways:
(this follows directly from the definition of conditional probability). Rearranging the terms in this chain of equations gives Bayes’ theorem
which can be used to compute the two relevant probabilities referred to by Self and Francois, i.e. Pr(L ∣ RaS) on the right-hand side and Pr(RaS ∣ L) on the left-hand side of the equation, respectively.
Here I concentrate on the right-hand side of the equation expressing Bayes’ theorem and, firstly, consider the easiest bit, which is the marginal probability of voting Leave. This is a known quantity, because it can be computed as the proportion of voters at the 2016 referendum who voted to leave the EU. Official data from the UK Electoral Commission give:
Next, I consider Pr(L ∣ RaS). In his statement, Self seems to indicate that he considers this probability to be essentially 1. During the exchange, Francois asks Self: “How do you know that in a secret ballot?”, which is of course a fair point. Self replies: “I suspect it”, which suggests some process of more or less formal probabilistic elicitation; if Self were a statistician, he might have decided to use a specific probability distribution to encode the subjective belief that the proportion of Leavers among racists and anti-Semites is tightly centered around a value that is close to the theoretical maximum of 1. For example, he could have used a Beta(96,4) distribution to model Pr(L ∣ RaS). This amounts to considering a fictional experiment in which Self randomly selects 100 racists and anti-Semites from the general population, asks them whether they voted Leave or Remain, and finds out that 96 of them voted Leave. Graphically, we could depict this distribution as in Figure 1, in which 99% of the probability is included in the interval [0.893; 0.993].
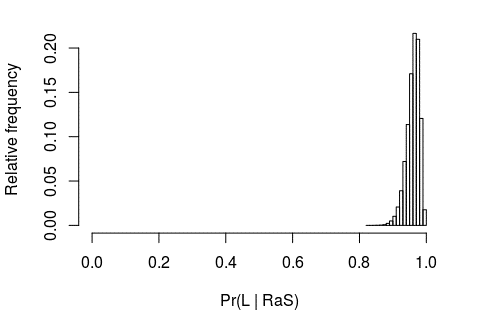
FIGURE 1 Subjective interpretation of Will Self’s assessment of the probability that a racist or anti-semite votes Leave.
Of course, this is not necessarily Self’s exact assessment – rather, it is my own subjective interpretation of his statement, in which he has included a measure of uncertainty, while expressing a strong belief that the proportion of Leavers among racists and anti-Semites is very close to 1. It is difficult to envisage an actual data collection exercise to inform this probability – it would be very complicated to select a random sample of racists and anti-Semites in order to survey their voting behaviour at the 2016 referendum. It is, however, important to recognise that statistical theory still allows us to model subjective belief in a probabilistic fashion – something we probably do more often than we realise.
This same reasoning applies when it comes to quantifying the population “prevalence” of racists and anti-Semites, Pr(RaS). While it is possible that data exist on this issue, I believe that accurate estimates are unlikely to be available, especially as Self’s premise conflates racists and anti-Semites (although, to be fair to him, he probably never intended for his ideas to be artificially modelled using probability and statistics). Thus, instead of trying to produce a single empirical estimate for Pr(RaS) in terms of a probability distribution, I will instead perform some sort of sensitivity analysis, by letting the probability vary in a suitable range and then computing the resulting value for Pr(RaS ∣ L).
In principle, Pr(RaS) can vary between 0 and 1. However, in this particular set up, its theoretical value is actually restricted to a smaller subset. This is due to the combination of two factors. Firstly, following Self’s premise, we are assuming that nearly all racists and anti-Semites voted Leave. Secondly, we know that slightly less than 52% of those who actively took part in the Brexit referendum voted Leave. Thus, the overall proportion of racists and anti-Semites in that population cannot exceed a theoretical upper bound of about 0.5. If this upper bound was exceeded, the resulting value for Pr(RaS ∣ L) would be greater than 1, which is impossible. For example, if we set Pr(RaS) = 0.7 then
While arguably the upper bound of 0.5 can be considered as unrealistically large, I will nevertheless perform the analysis over the mathematically valid range [0; 0.5]. Using the setup above, we can combine the uncertainty in Pr(L ∣ RaS), as expressed by the Beta(96,4) distribution, to that of Pr(RaS), defined as a grid of possible values between 0 and 0.5, as well as the known value for Pr(L) in order to obtain the resulting distribution Pr(RaS ∣ L), as a function of the assumed prevalence for racists and anti-Semites.
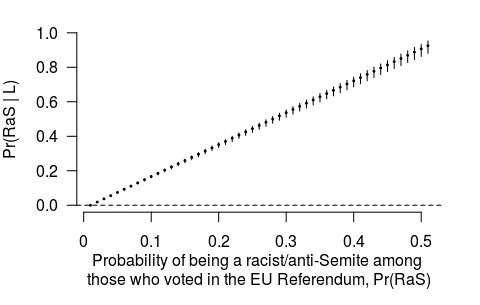
FIGURE 2 Probability of being a racist or anti-Semite among Leavers as a function of a range of theoretically possible values for the population prevalence of racists and anti-Semites.
Figure 2 shows a summary of the underlying probability distribution for Pr(RaS ∣ L), which is what Francois is referring to, in correspondence of each assumed value for Pr(RaS). Reading across the x-axis, it is possible to see the point estimate (represented as a dot) together with a measure of the spread of the distribution in terms of the 95% interval estimate (the vertical lines spanning either sides of the dots).
What we learn from this figure is this: even by assuming that virtually every racist and anti-Semite voted Leave, what Will Self was in fact implying with his statement is that only a proportion of Leave voters is racist and anti-Semite. This can be as little as 0%, in the ideal case where none of those voting is racist and anti-Semite, but the proportion increases to just below 20% (0.2) if we assume that 10% (0.1) of those voting are racist and anti-Semite. Only when the population prevalence of racists and anti-Semites is set as high as 50% (0.5) do we find the value for Pr(RaS ∣ L) approaching 1.
The importance of statistical literacy
The Self-Francois exchange may be considered a good example of the problems of modern politics. “Facts” and opinions are thrown at viewers and the general public, often without the necessary scrutiny. Arguments are twisted to score political points.
Some in the media are taking this issue seriously; they provide additional material in which the most important statements are thoroughly cross-examined, so as to determine the evidence backing up the various claims. But, of course, this does not always happen – or perhaps the fact-checking component does not receive the prominence that it deserves.
Based on the analysis developed above, it is possible to conclude that, unless you are willing to assume that over half of all Brexit referendum voters is racist and anti-Semite, Self has not tried to slur everybody who voted Leave as a bigot. He may be insinuating that a sizeable portion of Leave voters fall into this camp, but Francois has misrepresented the argument being made. Whether that was deliberate or not, we do not know.
Rather than twist the argument, Francois could have – and should have – pushed Self to discuss the evidence on which he made his claim. Self was relying on his own subjective judgement, but the beauty of statistical argument is that this does not prevent him from drawing inference and conclusions – although this should still be subject to both an explicit statement of the underlying assumptions and a clear quantification of the resulting uncertainty.
This example indicates that statistical literacy really ought to be a prerequisite for any form of social interaction, but especially politics.
About the author
Gianluca Baio is professor of statistics and health economics at University College London, and a member of the Significance Editorial Board.



