
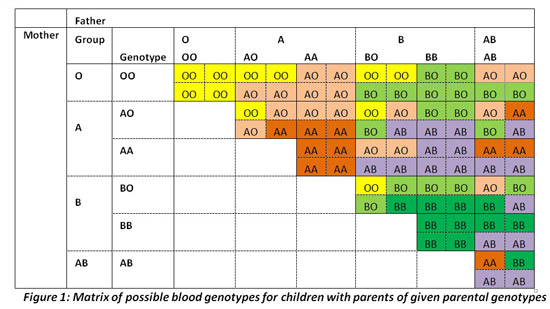
But what is it that determines an individual’s blood group? You inherit a piece of genetic information from both parents, comprising your blood genotype. Which one of the two pieces of information you inherit from each parent appears to be a random chance. There are six possible genotypes: OO, AO, AA, BO, BB and AB. If you have blood group O, your genotype must be OO (you did not inherit either A or B antigen from either parent). If you have group AB, then your genotype is AB: you must have inherited an A antigen from one parent and a B from the other. If you have group A, you could have inherited the antigen from both parents (in which case your genotype would be AA) or from one parent only, and neither the A nor B antigens from the other parent (in which case your genotype would be AO). A corresponding situation exists for Group B individuals, who may have genotype BO or BB. Note that genotypes AO and AA, and BO and BB, are not readily distinguishable from each other.
The matrix of possible blood groups that a child with parents of given genotypes may have is given in Figure 1. The outcomes recorded in each of the small sub-cells within a cell are equally likely.
In some cases we can use information from the blood group of children to estimate the likely genotype of their parents. Consider those who have blood group A to belong to a population, a certain proportion of which has genotype AO, with the remainder being AA. I will refer (rather loosely) to p as the probability that a particular individual (my wife), with known blood group A, but unknown genotype (we have no information about the blood groups of either of my wife’s parents), having genotype AO.
To estimate p (which could equally well be used to estimate the corresponding probability of a blood group B individual having genotype BO) I use Bayesian statistics, in which a personal belief in the likelihood of an event is modified by the acquisition of new information. I start with a 'prior' estimate of the value of the probability p. In the absence of other information I initially assume that p=0.5: i.e. that the AA and AO genotypes occur in the population with equal frequency. I will use actual observations from my own family to modify my 'prior' guess at p to derive a corresponding 'posterior' estimate.
Both my son and daughter have genotype AB, as I do. From Figure 2 below, you can see that the event of my son (our first child) having genotype AB could have occurred through either of two 'branches': each corresponding to my wife having either genotype AO or AA. And if we set p=0.5 initially, then the probability of occurrence of events leading to the observed outcome on the upper branch = 0.5×0.25 =0.125, and the probability of occurrence of events on the lower branch leading to the observed outcome is 0.5×0.5 = 0.25.
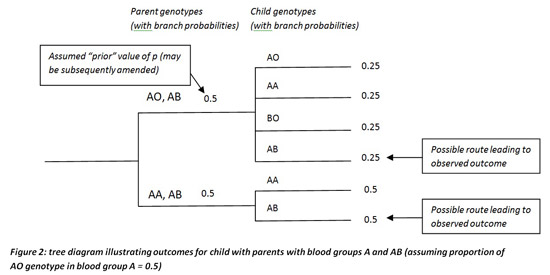
Hence under the prior assumption that p=0.5, the revised, 'posterior' estimate of the probability that my wife’s genotype is AO is 0.125/(0.125+0.25)=0.333.
I can revise the estimate a second time if more information comes my way. After our daughter was also found to have blood group AB, I reset our prior value of p to 0.333, and calculated that the probability of this event occurring from my wife having genotype AO is now 0.333×0.25=0.083, whereas the probability of this event occurring from my wife having genotype AA is 0.667×0.5=0.333. Hence my re-revised value of p is now 0.083/(0.083+0.333)=0.2.
We need not model the prior distribution of p as a constant. For example, under the prior assumption that p follows a uniform distribution, it may be shown that the estimate of the posterior probability following the determination of our son’s blood group is given by 0.273. Following the determination of our daughter’s blood group, this estimate would be revised to 0.158 (Note 1). Other alternatives to a uniform prior are also plausible: for example it may be possible to make a strong argument that low values of p (say) are more likely than high values.
So in summary, anyone who knows that their blood group is O or AB can state their blood genotype straightaway, as can some, but not all, of those who are group A or B and have some information to hand about their relatives’ blood groups. My own study on a very small sample has, after the arrival of two children with blood group AB, derived an estimate of the probability of a particular Group A individual of unknown genotype having genotype AO to be 0.2 under the assumption of a 'constant prior' (i.e. that genotypes AO and AA occur with equal frequency in the population); and an estimate of the probability of this same event to be 0.158 under the assumption of a 'uniform prior' (i.e. that the proportion of group A’s who are genotype AO is equally likely to be anything from 0 to 1). Other choices of prior will give different estimates. However, I cannot really claim that either of the values I have calculated are particularly likely to reflect the proportion of AO genotypes amongst the millions of Group A folk knocking around – of course, I have only sampled one individual!
References
-
Note 1: We can write a general expression for posterior probability as a function of prior probability p:
-
Under the assumption of a uniform distribution, the mean value of the above expression for the posterior probability, E(p) is given by the expression:
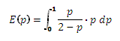
-
This expression can be solved using, for example, integration by substitution to give:
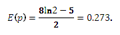
- If this value is then considered to be the (constant) prior value of p, then the revised estimate of the posterior probability is given by 0.273 / (2 – 0.273) = 0.158.




