
The headline changes are: 1) The addition of a new £1 million raffle prize, 2) the addition of a new prize tier for matching two numbers (a free ticket for a future draw) and 3) an increase in the number of balls from which the winning numbers are drawn, from 49 to 59.
Camelot have been quick to highlight the benefits of this new arrangment: an increased chance of 'winning a prize' (from 1 in 54 to 1 in 9.3) and an increased chance of becoming a millionaire (from 1 in 14 million to 1 in 10 million). It all sounds pretty good until you realise that, by increasing the number of balls from 49 to 59, the odds of winning most prizes have lengthened considerably (your chances of scooping the jackpot have increased from an already optimistic 1 in 14 million to a rather more spectacular 1 in 45 million).
However, the clever introduction of a free lottery ticket for matching two numbers brings the odds of winning anything crashing back down to under 1 in 10. Indeed, your chance of matching two numbers is a fairly healthy 1 in 10.3. The introduction of a new £1 million 'raffle prize', meanwhile, helps keep your millionaire chances within reach (if you fancy your chances at tossing 23 heads in a row, for instance).
How do the changes affect the weekly lottery player?
All these odds distract from a more practical consideration: your long-term expected winnings. In other words, how much of a return can you expect in the long run for your weekly lottery investment? Conveniently, the regulatory commission report notes, 'The new prize structure should tend towards an average prize payout percentage of 47.5%, as it is currently.' Saving us statisticians from any complex calculations.
This means that for every £2 ticket you buy, you should on average get 47.5% (or 95 pence) back. Many question this as an investment – with lotteries being a 'tax on the stupid' a common remark – but my view is that players are paying a little over a quid for the fun of taking part, and to a lot of people that represents perfectly good value.
However, if we dig a little deeper, things become a little less clear. That average prize payout percentage presumably includes those new free tickets, of which there are likely to be a lot, given the low odds of winning one. Who's paying for these 'free' tickets? The Commission report states that: 'The full cost of the free tickets will be met from the prize fund for each draw'.
This raises a curious possibility. If 10 million tickets are sold under the current system, that generates £20 million in sales, which means (if we're generous and round up the prize fund to 50% of sales) £10 million will be given back to players in prizes. The new system, meanwhile, would see around 1 in 10 of those players – so 1 million – winning a free ticket, which Camelot values at £2 million (£2 per ticket). That £2 million then comes out of the prize fund, leaving just £8 million in prizes and placing that leftover cash in some sort of limbo, waiting to be 'claimed' by the winners to participate in some future draw.
What happens next, however, is vague. The report states that: 'In line with the retention model agreed for the third licence, a proportion of the proceeds from those lucky dip 'sales' will flow both to Camelot and Good Causes in the normal retention proportions.' My reading of this is that if all 1 million free tickets are claimed at the next draw, Camelot will take that £2 million fund and put it towards the sales figure – not the prize fund – for that draw.
Intuitively, this seems like it makes perfect sense: Camelot are in effect saying to those 1 million winners, 'Look, here's your two quid, but we're going to buy you a £2 lottery ticket with it instead!'. But this misses a crucial point: if your expected return on a £2 ticket is only £1, then it's only 'worth' £1 in a purely fiscal sense, which means £1 has gone somewhere.
Let's consider a hypothetical example. Suppose I'm the only person buying lottery tickets, and I decide that over the next two weeks I want to play 10 million times in each Saturday night draw. Under the current system (and again assuming a 50% payout) I'd spend £20 million on the first draw, and would expect to win the entire prize fund of £10 million. Next week I'd do the same thing, and over the two draws I'd have paid in £40 million and received £20 million in prizes: a 50% return on my questionable investment.
Under the new system, meanwhile, I again pay £20 million into the first draw, which generates a prize fund of £10 million, just as before. This time, though, 1 million of my tickets match two numbers earning me 1 million 'free plays', and so Camelot sets aside £2 million of the prize fund in case I want to use them next week. This leaves £8 million left in cash prizes to lower my bank manager's heart rate. At the next draw, I pay for 9 million tickets at a cost of £18 million to me, and use my 1 million free tickets from the last draw. Camelot 'pays in' these tickets as £2 million in sales, and so the sales fund is again £20 million, with £10 million sitting in the prize pot. This time, by some remarkable fortune, I don't win any of those pesky free tickets and instead pocket the full prize fund of £10 million. Under this new system I've paid out £38 million over the two draws, but have received only £18 million back in cold hard cash: a 47% return on my investment.
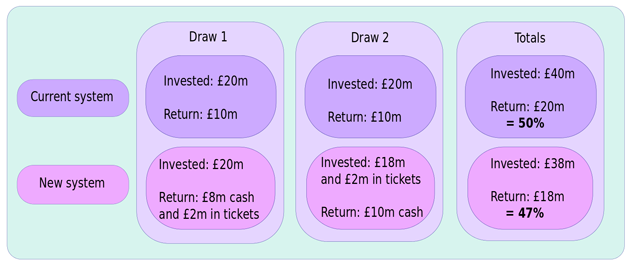
This is, of course, quite an extreme example, but by supposing I don't win any free tickets on the second draw I'm being as kind as possible to the new system: obviously I'd have won even less cash if any of my tickets had matched just two numbers, as each of those 'wins' takes £2 out of the (cash) prize pot.
This illustrates how complicated lotteries can be and this is just one probabilistic angle on the information Camelot have provided. You could also discuss whether a 1 in 10 chance of winning another go, or a fractionally increased chance of becoming a millionaire really does make up for the (much) longer odds on the more desirable cash prizes. For some, of course, it will and Camelot themselves claim that 'the majority of players are more interested in prizes than the odds of the game'. This is the idea of 'utility': how much value we personally ascribe to various outcomes. For example, to many people the thrill of winning a free ticket will be worth more than the £2 it costs to play.
Most importantly of all, however, this shows how much can hide under the surface of a glossy commercial or a press release. That said, their marketing team does deserve some credit: it takes a uniquely creative mind to market lower odds as simply 'more numbers to choose from!'.




