
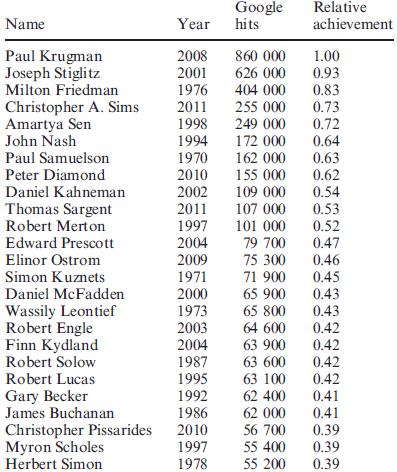
- Claes, A.G. P. and De Ceuster M. J. K. (2013) Estimating the economics Nobel Prize laureates’ achievement from their fame, Applied Economics Letters, 29, 884-888 http://dx.doi.org/10.1080/13504851.2012.758836
- Simkin, M. V. and Roychowdhury, V. P. (2011) Von Richthofen, Einstein and the AGA, Estimating Achievement from Fame, Significance, 8, 22–6. http://onlinelibrary.wiley.com/doi/10.1111/j.1740-9713.2011.00473.x/abstract
- Varian, H. (1999) Intermediate Microeconomics. W.W. Norton & Company. New York.
- Nash, J. (1951) Non-Cooperative Games. Annals of Mathematics 54, 286-295 http://www.jstor.org/stable/1969529




