
During his 26 March call into “The Sean Hannity Show” on Fox News, President Donald Trump questioned whether New York state would actually need the tens of thousands of ventilators its state’s leaders had estimated would be necessary to deal with its expected number of coronavirus cases. Then, three days later during a briefing at the White House, Trump said: “Something’s going on, and you ought to look into it as reporters. Where are the masks going? Are they going out the back door? How do you go from 10,000 to 300,000?”
He later added: “We do have a problem of hoarding. We have some health care workers, some hospitals, frankly — individual hospitals and hospital chains — we have them hoarding equipment, including ventilators. We have to release those ventilators, especially hospitals that are never going to use them. They have to release them.”
This Presidential dismissal of the magnitude of these numbers may be indicative of a lack of understanding or disregard of exponential growth that plagues a large portion of the population. Even many who are well educated do not understand the concept, and often use the term “exponential growth” or “exponentially” as hyperbole rather than as a description of a trend in growth or acceleration (see Dr Manil Suri’s New York Times opinion piece for an interesting discussion of this issue). Even many of those who have spent a lifetime in the world of business and finance may not see that compound interest is actually exponential growth (or, if an investor is unfortunate, exponential decay).
Why should we care about a seemingly arcane mathematical principle? Because under our current circumstances, misunderstanding or disregard of exponential growth and the decisions made based on this misunderstanding or disregard may have extremely grave consequences.
Albert A. Bartlett (1923-2013), who was professor emeritus in nuclear physics at University of Colorado at Boulder, flatly stated: “The greatest shortcoming of the human race is our inability to understand the exponential function.” Three months ago, I would have agreed with Professor Bartlett’s general message, but I also would have thought he was exaggerating its importance. However, the impact this lack of understanding is having during the coronavirus pandemic has quickly brought me in line with Professor Bartlett’s position on the importance of this issue.
To explain exponential growth, let’s make a deal. I will clean your home, flat, or apartment every day in May 2020 (31 days) if you pay me one penny (1/100th of a US Dollar) on the first day and triple what you pay in every ensuing day. Is this deal tempting? Perhaps you’re thinking, “I won’t have to clean my home for four weeks, and it will only cost me a few pennies, maybe a few dollars max! Where do I sign up?”
But if that is what you are thinking, you’re in for a nasty surprise. With exponential growth, in 31 days my daily rate goes from $0.01 to more than $2 trillion. If we amend our deal so you only double what you pay me each day, your final bill is reduced to $10 million, and if we amend the deal so you only increase what you pay me by 50% each day, your final bill is a much more reasonable $1,917.51.
The following table summarizes these results:
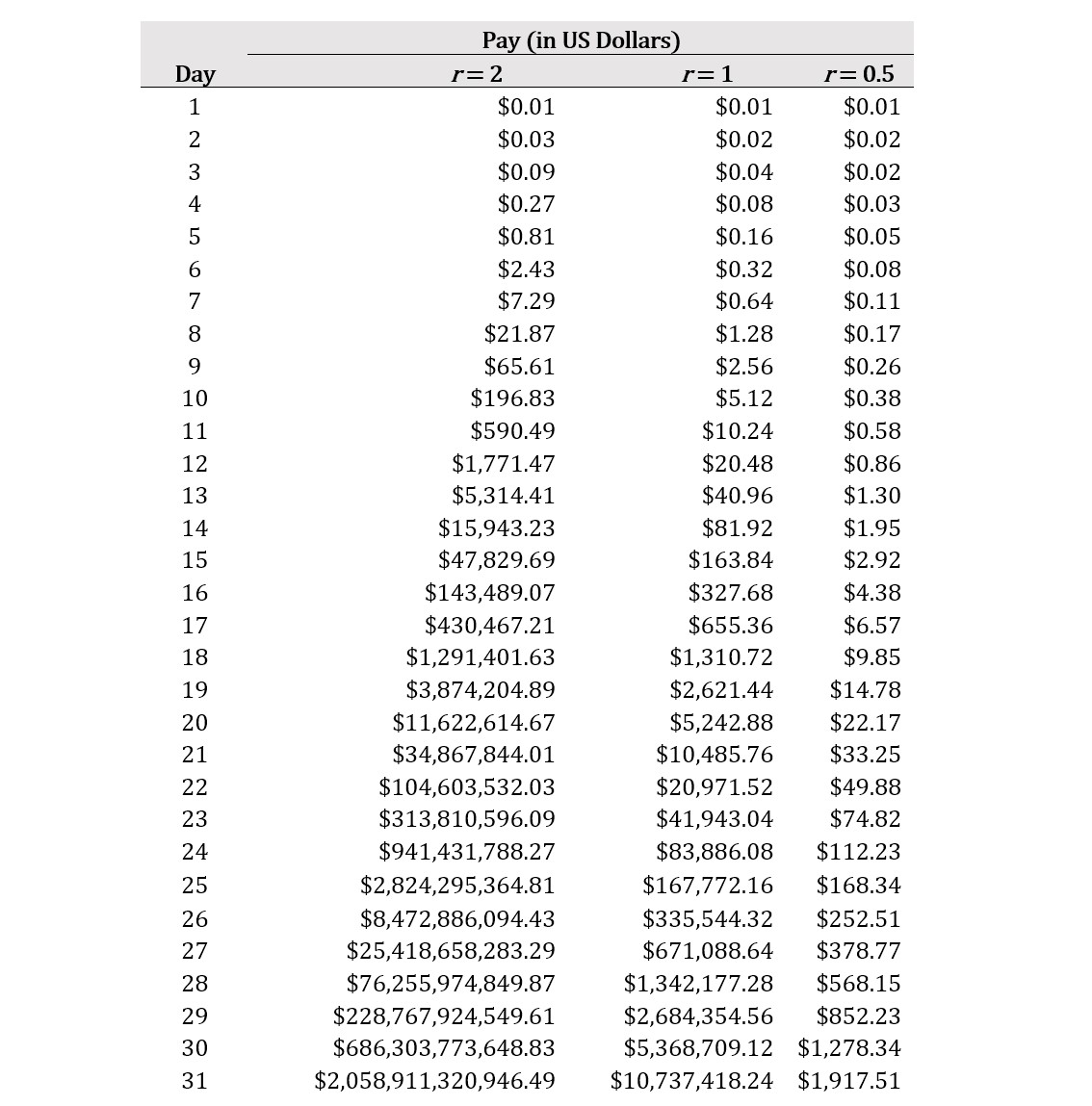
In the table, r refers to the growth rate, and the formula for exponential growth of a variable x at growth rate r (or the proportion of growth in each of t) increments is:
xt = (1+r)tx0
In this formula, x0 and xt represent the initial value of our variable x and the value of our variable x after t increments, respectively. In the example where my pay for cleaning your home triples each day, r = 2, x0 = 0.01 (my starting rate) and t = 30 (that is, day 1 to day 31 represents 30 time increments). We then have:
xt = (1+2)30(0.01) = 2,058,911,320,946.49.
The following series of graphs illustrate the nature of exponential growth.
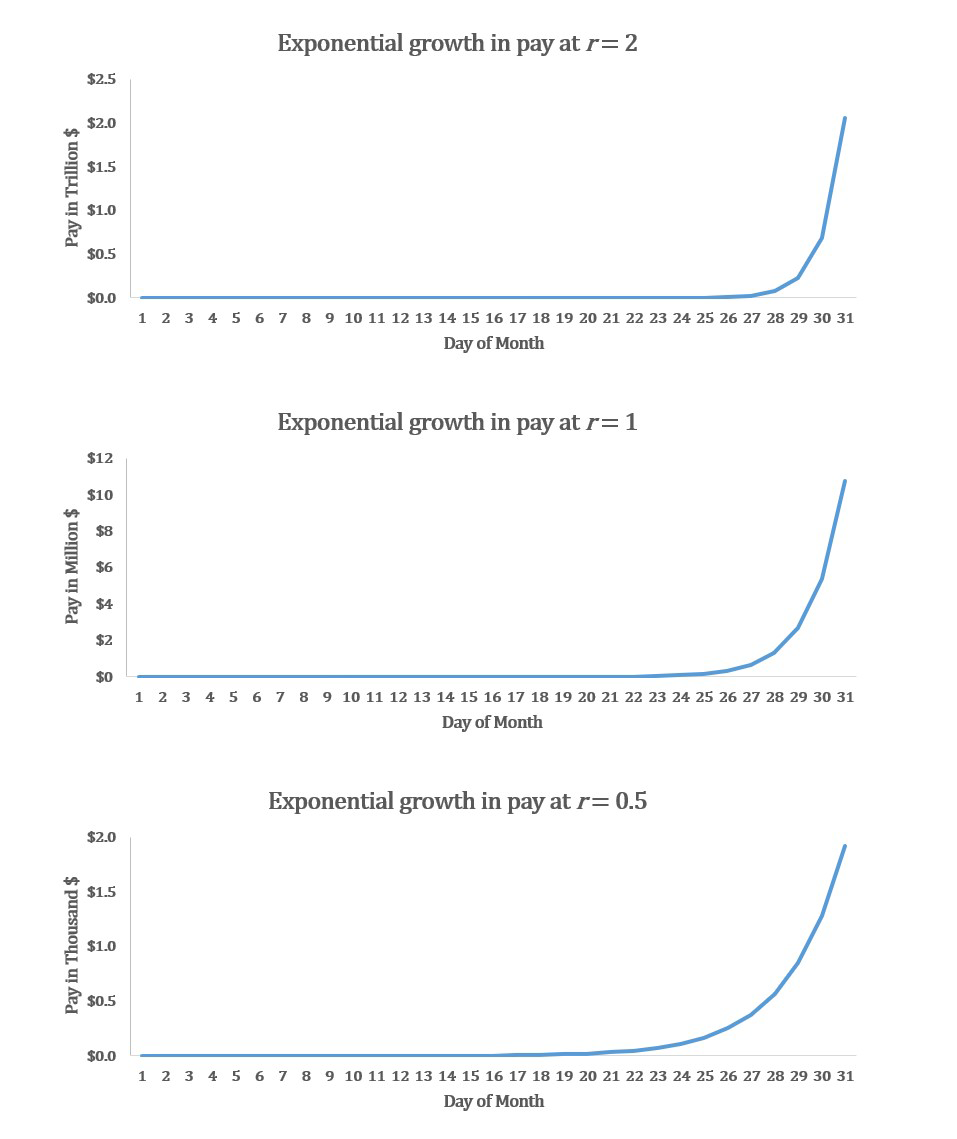
We couldn’t place each of these exponential growth curves on a single graph because the values on the y-axis of the r = 2 example would dwarf the r = 1 and r = 0.5 examples, but these three graphs do show the same pattern: it takes a few weeks for growth to take off, but when it does, the amount you owe me explodes.
How does this discussion apply to a pandemic? If the need for masks starts at x0 = 10,000, how many increments or time periods t will it take to reach xt = 300,000? That depends on the growth rate r. The following table shows how many increments or time periods t it will take to reach the need for at least 300,000 masks at various growth rates r per increment or time period.
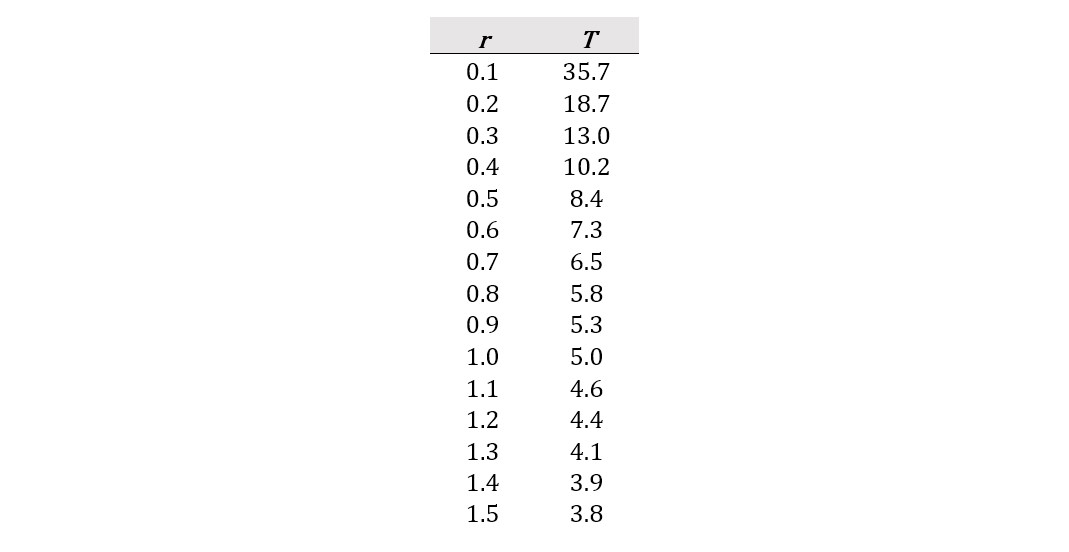
If r = 1, the need for masks increases by 100% (doubles) every increment or time period t, and we go from needing 10,000 masks to needing at least 300,000 masks in five time periods. If the need for masks doubles every week, the need for masks will go from 10,000 to over 300,000 in five weeks. If the need for masks doubles every three days, the need for masks goes from 10,000 to over 300,000 in 15 days. And if the need for masks doubles every day, the need for masks goes from 10,000 to over 300,000 in five days.
If the growth rate r is slower, it will take more increments or time periods t to go from a need for 10,000 masks to a need for 300,000 masks. For example, if r = 0.5, this means the need for masks is increasing by a factor of 1.5 per increment or time period t, and the need for masks goes from 10,000 to over 300,000 masks in 8.4 time periods. If the need for masks increases by a factor of 1.5 every week, the need for masks goes from 10,000 to over 300,000 in 8.4 weeks. If the need for masks increases by a factor of 1.5 every three days, the need for masks goes from 10,000 to over 300,000 in less than four weeks. And if the need for masks increases by a factor of 1.5 every day, the need for masks goes from 10,000 to over 300,000 in less than nine days.
So, even under relatively slow progression of the coronavirus, we can move from a need for 10,000 masks to a need for over 300,000 masks rather quickly. Exponential growth explains how an outbreak grows into an epidemic and eventually becomes a pandemic.
The large increases in the needs for masks and ventilators are not due to hoarding. They are easily explained and understood through exponential growth.
Another example of how exponential growth can influence the spread of the coronavirus is exponential spread of information. Suppose two people, perhaps because of their shared misunderstanding of how pandemics develop, each share some false information (perhaps that the coronavirus pandemic is a politically motivated hoax, or that it will magically disappear in April) with two unique acquaintances. Now suppose that these four people each share this false information with two unique acquaintances within one hour, and then those acquaintances each share this false information with two unique acquaintances within one hour, and so on. Through this process, this misinformation will spread to over 33.5 million people in only 24 hours.
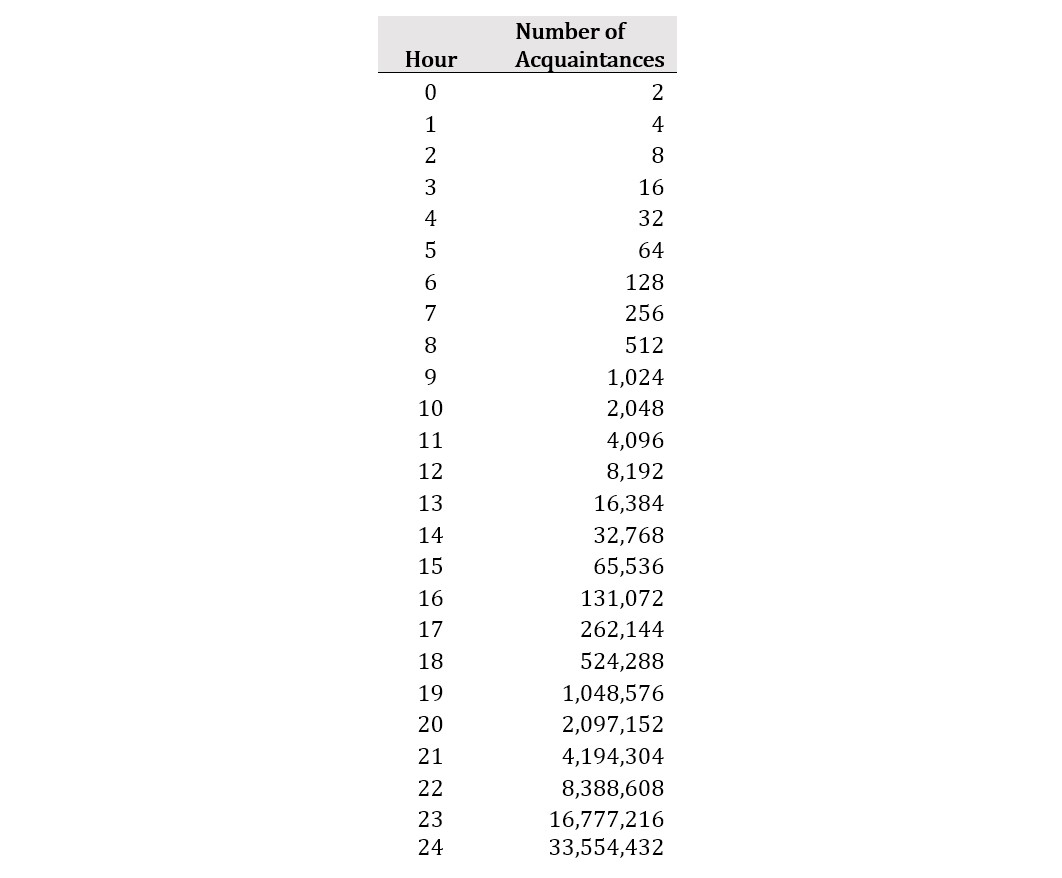
That total far exceeds (in most cases, is at least double) the estimated 2020 population of each of the 48 European nations except Russia, Germany, the United Kingdom, France, Italy, Spain, Ukraine, and Poland. This is why those who have public platforms and eager audiences must be extremely careful about what they say with regard to this pandemic. On a more positive note, the capacity exists for timely and appropriate knowledge to spread similarly, and exponential growth can potentially be used to combat and mitigate bad information.
Exponential growth is a powerful concept, and lack of understanding or outright disregard for the concept can lead to very poor decision-making and potentially dangerous and deleterious outcomes – especially during a global pandemic. For the sake of each of us, and especially for the sake of the most vulnerable and impoverished of us, let’s hope the message is now getting through.
About the author
James J. Cochran is associate dean for research, professor of applied statistics, and the Rogers-Spivey faculty fellow at the Culverhouse College of Business, University of Alabama. He is vice-chair of the Significance Editorial Board.



