
Net Foreign Income (NFI) is the difference between GNP and GDP; this shows the net flow of money between a given country and the rest of the world. In the case of Ireland, it reveals an alarming reality that many commentators overlook.
Since 1975, NFI has been negative and represents the net outflow of money from Ireland. This is made up of three different kinds of funds leaving the country. First is the repatriation of profits by foreign-owned companies. Second is the royalties and licensing fees to those companies and thirdly the payment for research and development carried out by them.
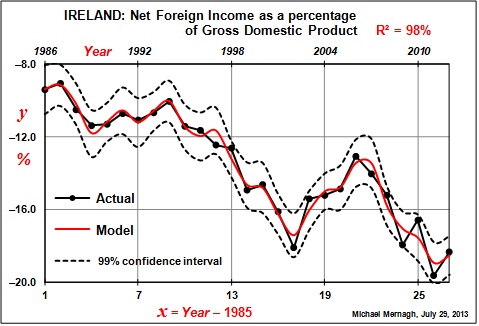
Prior to 1986, those outflows were not accurately quantifiable, they disappeared into a sort of statistical “black hole”. In 1986, NFI in the Irish economy became more reliably verifiable when it stood at minus €2.5 Billion (about minus 10% of GDP). From this point onwards, it has followed a downward trend. By 2011, it had fallen to minus €32 Billion (or minus 20% of GDP).
The conventional economic wisdom that has taken hold in Ireland is that it needs to allow multinational companies to take enormous sums of money out of the country to compete in the modern world. This in turn will attract foreign investment to create jobs for a growing population. Ireland’s best selling point is a well-educated and technically competent workforce. The main sectors for jobs growth have been the modern high-tech industries of pharmaceuticals and information technology. However, growth in these areas has relied heavily on foreign multinationals opening up these positions instead of Irish owned and operated companies.
The graph below demonstrates how the minus figure that represents NFI has grown over the period of 1986 to 2011.
Taking the model into the future, it indicates to us that NFI could equal 100% of GDP by the middle of the 23rd century as shown below.
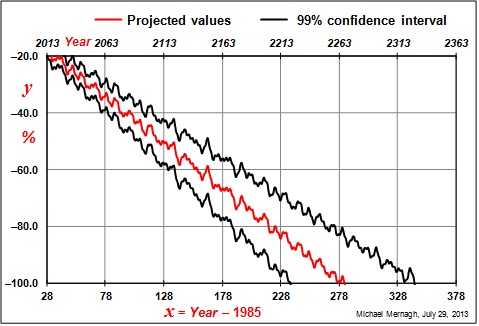
What this shows is that Ireland’s reliance on foreign investment will not provide a sustainable economic future and diversification is becoming essential to the economy. To illustrate this I will end with an anecdote. The Neutral Zone was an episode in the popular science fiction television series of Star Trek — The Next Generation.
In that episode, a salesman from late 20th century Earth is cryogenically frozen and sent into deep space. He is intercepted by the Starship Enterprise in the 24th century. When awakened, the salesman immediately starts to estimate how much wealth his investments have accumulated over three centuries or so. However, he is then shocked to discover that the concept of private property no longer exists in the 24th century.



